나왔사와여
문제(출처 : <이것이 코딩 테스트다> )

답안지
이번 주차에서는 최단 경로 알고리즘에 관해 배웠는데. 최단 경로부터 가물가물해서. 옛날에 하던 핸드 시뮬레이션을 했다. 그리고 답은 답안지를 베낀 것임. 제가 푼 것 XXXXX
# 값 초기화, 원래 코드는 입력 받는건데, 일일이 입력받기 귀찮아서 명시해줌
INF = int(1e9)
# n=회사(노드) 개수, m=회사끼리 연결된 도로(간선) 개수
n, m = 5, 7
graph = [[INF]*(n+1) for _ in range(n+1)]
# 각 간선에 대한 정보를 입력받아 그 값으로 초기화
graph[1][2] = 1; graph[2][1] = 1;
graph[1][3] = 1; graph[3][1] = 1;
graph[1][4] = 1; graph[4][1] = 1;
graph[2][4] = 1; graph[4][2] = 1;
graph[3][4] = 1; graph[4][3] = 1;
graph[3][5] = 1; graph[5][3] = 1;
graph[4][5] = 1; graph[5][4] = 1;
# 방문판매 회사 X와 소개팅할 회사 K
x, k = 4, 5
# 자기 자신에게 가는 비용은 0으로 초기화
for a in range(1, n+1):
for b in range(1, n+1):
if a==b: graph[a][b]=0
# 플로이드 워셜
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])
print(k, a,b, graph)
distance = graph[1][k]+graph[k][x] # 1= a회사, k = 소개팅 회사, x = 방문판매활 회사
# 못 가는 경우 -1 출력
if distance >= INF: print(-1)
else: print(distance)
분석
플로이드 와샬 메인 코드다.
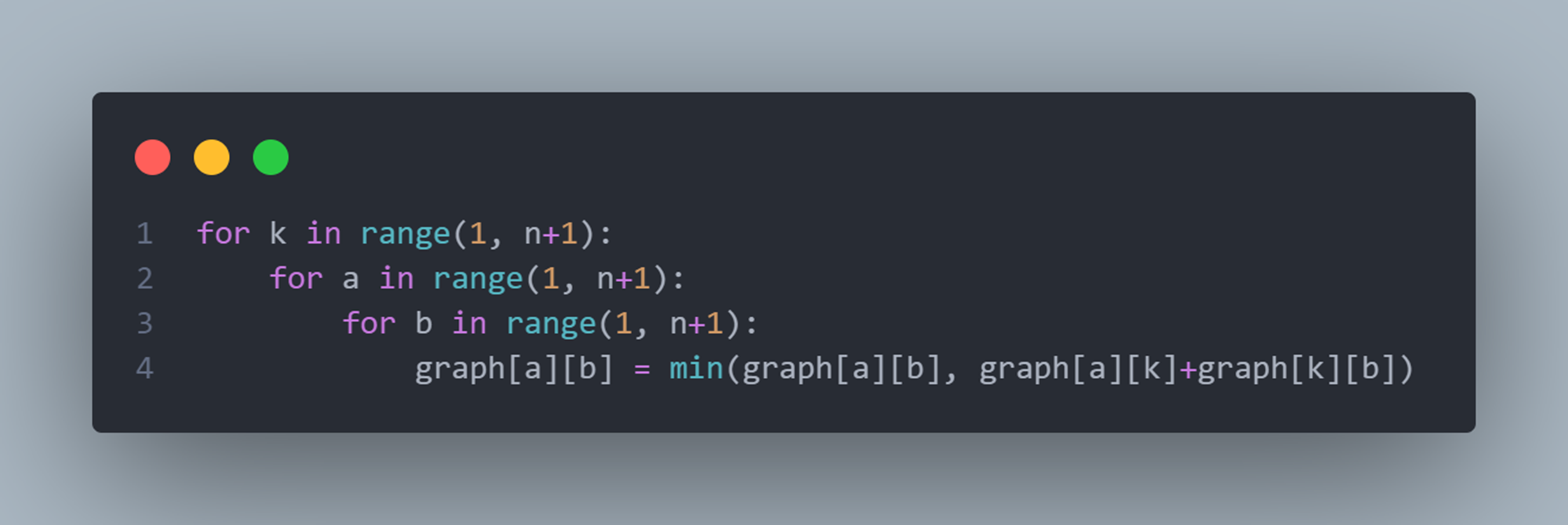
1. 1부터 시작하는 이유는 노드 번호를 맞추기 위함이다. 노드가 1번부터 시작하니까...ㅇㅇㅇ
2. 4번 코드는 개인적인 생각으로 아래와 같다 (아닐 수도 있으니까 흘려들을 것)
- graph[a][b] : a노드에서 b노드로 가는 가중치
- graph[a][k] + graph[k][b] : a노드에서 k노드에 갔다가 k노드에서 b로 가는 가중치 합
예를 들어서 아래 그래프에서 5에서 3을 가고 싶다고 가정하자. (노드가 3개, 간선이 3개다. 나머지 지저분한 선은 무시함)
그럼 2가지 방법이 있다.
1. 5노드에서 3번 노드로 한 번에 가기. 이런 경우 가중치는 10이다.
2. 5노드에서 4번 노드에 갔다가, 4번 노드에서 3번 노드로 가기. 이런 경우 가중치는 7이다.
그렇다면 최단 경로 문제에서는 가장 가중치 값이 적은 방향을 선택하기 때문에 2번을 선택하게 된다.
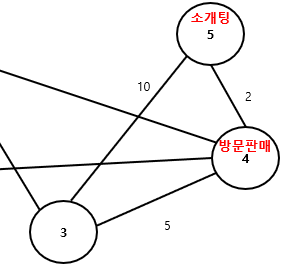
보통은(?) 간선마다의 가중치 값이 다른데, 이 문제에서는 1로 통일해서 좀 헷갈릴 수 있을 것 같다.
가쟈
% 주의 아래부터는 소곡이가 이거 공부할 때 쓴 방법임%
일단 이런 그래프가 있고 1번에서 4번으로 가는 최단 경로를 알고 싶다고 하자.
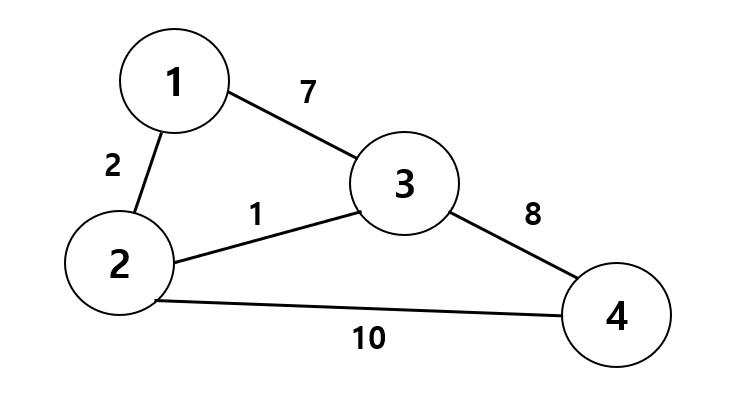
값 초기화
그래프는 아래와 같이 그릴 수 있다.
플로이드 와샬은 모든 노드에서 모든 노드로의 최단 경로를 그리다보니 이렇게 2차원 배열로 그린다. 머리아프게 왜 2차원 배열을 쓰지...? 싶겠지만.

나는 간단하게 행이 현재 노드이고 열이 방문할 노드라고 생각하고 있다.
2차원 배열은 아래와 같이 채운다.
- 자기 자신은 가중치가 0이다. ex) (1,1), (2,2), (3,3), (4,4)
- 대각선을 제외한 곳은 모두 INF(무한)으로 채운다.
- 그리고 간선의 가중치를 넣어준다. 양방향이기 때문에 행과 열의 숫자를 바꿔서도 입력해준다. ex) (1,2)->(2,1)의 간선의 가중치가 2 이므로 둘 다 2를 넣어준다.
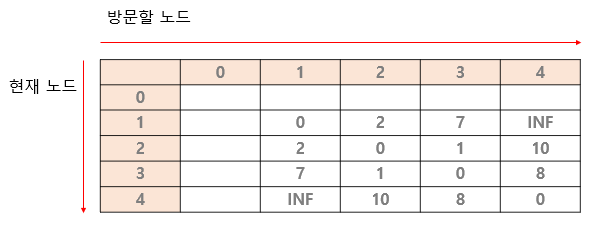
헤헤헿헤
이제 그냥 코드만 실행하면 됨

3중 for문은 가독성이 매우 떨어지지만 잘 생각해보면 매우 쉽다
- k = 소곡이가 b지점까지 갈 때 거쳐갈 수 있는 곳
- a = 현재 소곡이가 서있는 곳
- b = 소곡이가 가고 싶은 곳
첫 회전에서는 다 1이기 때문에 딱히 변하지 않는다.
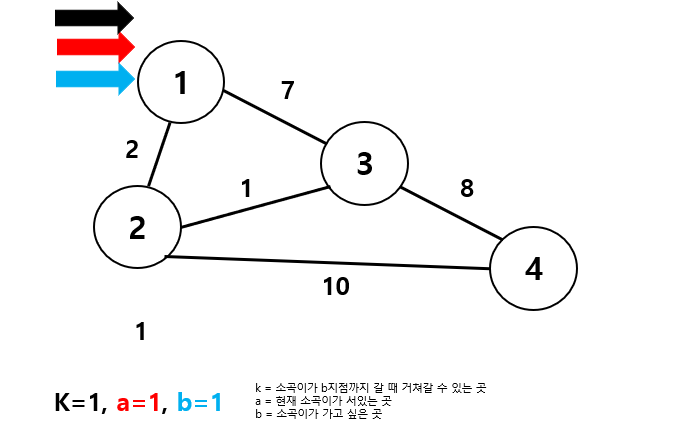
2회전과 3회전도.. 딱히...
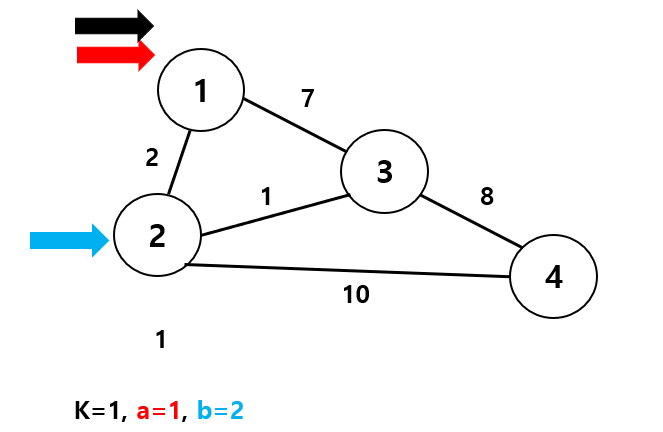
4회전에서는 빨간색 화살표(1)에서 파란색 화살표(4)로 이어지는 간선은 없지만, 거쳐갈 노드인 검은색 화살표(1)가 빨간색 화살표(1)와 같기 때문에 업데이트 시킬 방법이 없다.
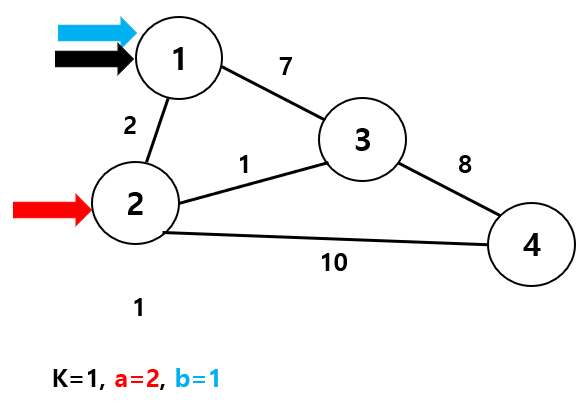
중간 for문을 2로 업데이트하면 이제는 2번 노드에서 1번 노드로 가야 한다.
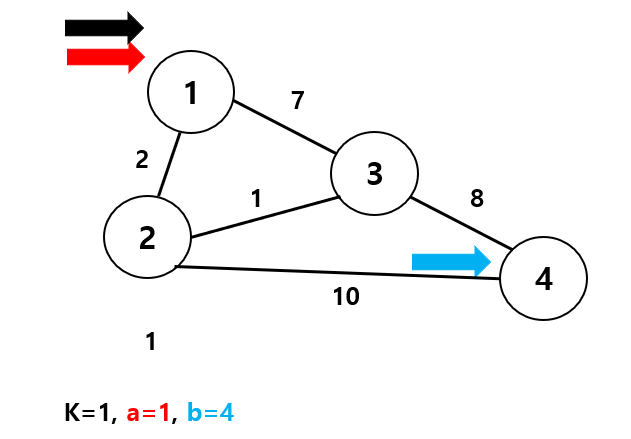
지금생각해보니까 문제를 좀 더 생각하고 만들 걸 그랬다. 다 똑같으니까 변하는 부분으로 넘어갈게요!!!

1번에서 3번 노드로 갈 때, 한 번에 가는 것(7)보다 2번 노드를 거쳐서 가는게(3) 가중치가 더 적죠??
- 2번 노드를 거쳐 간다는 것 = 1번 노드->2번 노드(가중치2), 2번노드->3번 노드(가중치1)
- 즉, 2+1 = 3
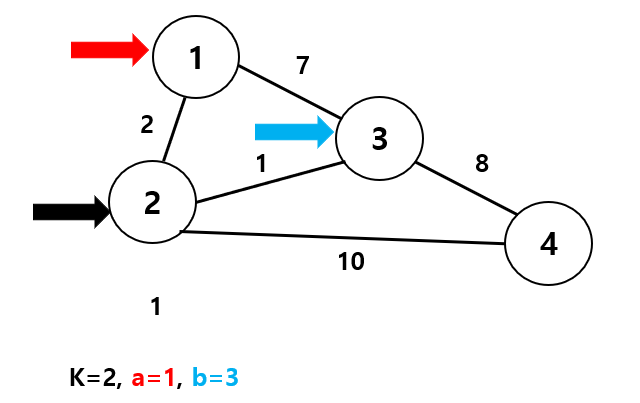
이 때 아까 가중치 배열을 업데이트 해줍니다. 왜냐면 최단 경로를 발견했으니까!!!
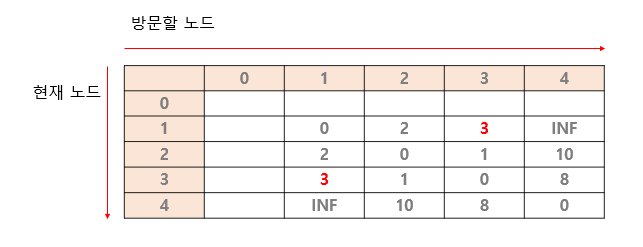
한 번 더 해봅시당. 이제는 1번 노드에서 4번 노드로 가야하는데. 3번 노드를 거치는 경우입니다.
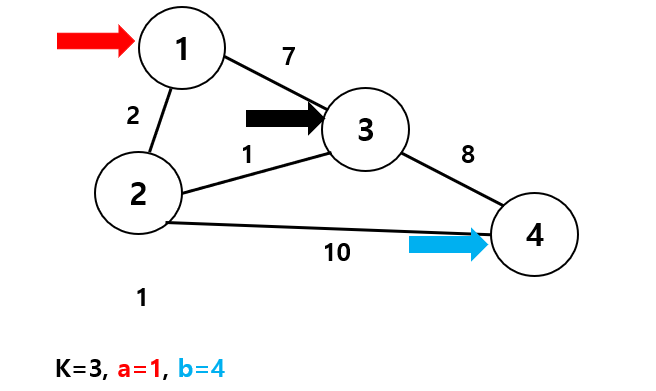
이번에는 코드를 곁들여서 봐봅시다. 여기서 graph는 우리가 앞서 만든, 간선의 가중치 값이 들어있는 2차원 배열입니다.
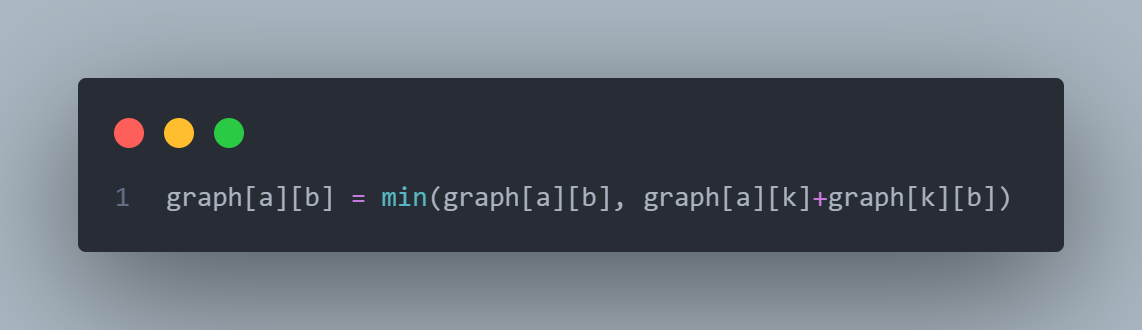
코드를 해석하면
- a에서 b로 갈 건데 -> graph[a][b]
- a에서 b로 바로 가는 거랑 -> graph[a][b]
- k를 거쳐서(a에서 k를 갔다가, k에서 b로 감) 가는 거랑 ->graph[a][k] + graph[k][b]
- 둘 중에 뭐가 더 가중치가 적은지(=더 빠른 지)

자, 현재 k=3, a=1, b=4니까,
- a에서 b로 바로 가는 경우는 graph[1][4] = INF가 됩니다. 무한이니까 가장 크겠쥬?
- k를 거쳐서 가는 경우는 graph[1][3] + graph[3][4] = 3 + 8 =11이 됩니다.
- 무한과 11을 비교해서 더 작은 수는 당연히 11이니까, (1,4)와 (4,1)은 11로 업데이트가 됩니다.

이해가 잘 안 되신다면 손으로 3중 for문을 돌려보면 이해가 쉬울 것입니다... 물론 그러면 그래프를 한 100번 그려야 되니까 ppt로 슬라이드 추가하면서 보는 거 추천.
끗
'python > 23년도 겨울 방학 코딩 스터디' 카테고리의 다른 글
| [이코테] part 3_3주차_p.323 문자열 압축 (3) (1) | 2023.02.01 |
|---|---|
| [이코테] part 3_3주차_p.322 문자열 재정렬 (2) (0) | 2023.02.01 |
| [이코테] part 3_3주차_p.321 럭키 스트레이트 (1) (0) | 2023.02.01 |
| [이코테] part 2_2주차_p.201 떡볶이 떡 만들기 (0) | 2023.02.01 |
| [이코테] part 2_3주차_p.99 1이 될 때까지 (0) | 2023.02.01 |



