#c언어로 쉽게 풀어쓴 자료구조 연습문제를 파이썬 코드로 구현
MAX_QUEUE_SIZE=10
MAX_VERITICES=10 #정점
class GraphNode:
def __init__(self, v=None, link=None):
self.vertex=v
self.link=link
class CircleQueue:
def __init__(self):
self.front=0; self.rear=0
self.queue=[None]*MAX_QUEUE_SIZE
def is_empty(self):
return self.front==self.rear
def is_full(self):
return (self.rear+1)%MAX_QUEUE_SIZE==self.front
def enqueue(self, data):
if self.is_full():
print('큐가 포화상태입니다.'); return
self.rear=(self.rear+1)%MAX_QUEUE_SIZE
self.queue[self.rear]=data
def dequeue(self):
if self.is_empty():
print('큐가 공백상태입니다.'); return
self.front=(self.front+1)%MAX_QUEUE_SIZE
return self.queue[self.front]
class BFS:
def __init__(self):
self.veritices_number=0 #정점의 개수
self.adj_list=[None]*MAX_VERITICES
self.visited=[False]*MAX_VERITICES
def insert_vertex(self): #정점 삽입
if (self.veritices_number+1)>MAX_VERITICES:
print('그래프: 정점의 개수 초가')
return
self.veritices_number+=1
def insert_edge(self, u, v): #간선 삽입
if (u>=self.veritices_number and v>=self.veritices_number):
print('그래프: 정점 번호 오류')
return
node1=GraphNode(v) #현재 정점(u)에 인접 정점(v) 연결
if self.adj_list[u]==None:
self.adj_list[u]=node1
else:
n1=self.adj_list[u]
while n1.link is not None:
n1=n1.link
n1.link=node1
node2=GraphNode(u) #인접 정점(v)에도 현재 정점(u)을 연결, 무방향 그래프
if self.adj_list[v]==None:
self.adj_list[v]=node2
else:
n2=self.adj_list[v]
while n2.link is not None:
n2=n2.link
n2.link=node2
def bfs_list(self, v=0):
Q=CircleQueue()
self.visited[v]=True #정점 v에 방문 표시
print('{} 방문 -> '.format(v), end=' ')
Q.enqueue(v) #시작 정점을 큐에 저장
while not(Q.is_empty()):
v=Q.dequeue()
w=self.adj_list[v]
while w is not None:
if not(self.visited[w.vertex]):
self.visited[w.vertex]=True #방문 표시
print('{} 방문 -> '.format(w.vertex), end=' ')
Q.enqueue(w.vertex)
w=w.link
if __name__=='__main__':
bfs=BFS()
for i in range(6):
bfs.insert_vertex()
bfs.insert_edge(0,2)
bfs.insert_edge(2,1)
bfs.insert_edge(2,3)
bfs.insert_edge(0,4)
bfs.insert_edge(4,5)
bfs.insert_edge(1,5)
print('**********너비 우선 탐색********')
bfs.bfs_list()
생각해보니까 나 전과했으니까 문과생이 아니라 전과생이라고 써야되나??? 훔...
다시, 문과생전과생이 이해한 파이썬 BFS(너비 우선 탐색)- 인접 행렬 버전 시작합니당!!
<인접 행렬 버전과 비교햇을 때 다른 점>
1. 초기화> 간선 연결 리스트(행렬->연결리스트)
2. 간선 연결 함수
3. 탐색 함수
<특징>

연결 리스트를 사용했지만 해싱인 것 같다. 초기화된 1차원 리스트 adj_list[현재 정점]에 인접 정점들을 연결리스트로 연결하는 것이 원리다.
<간선 연결>
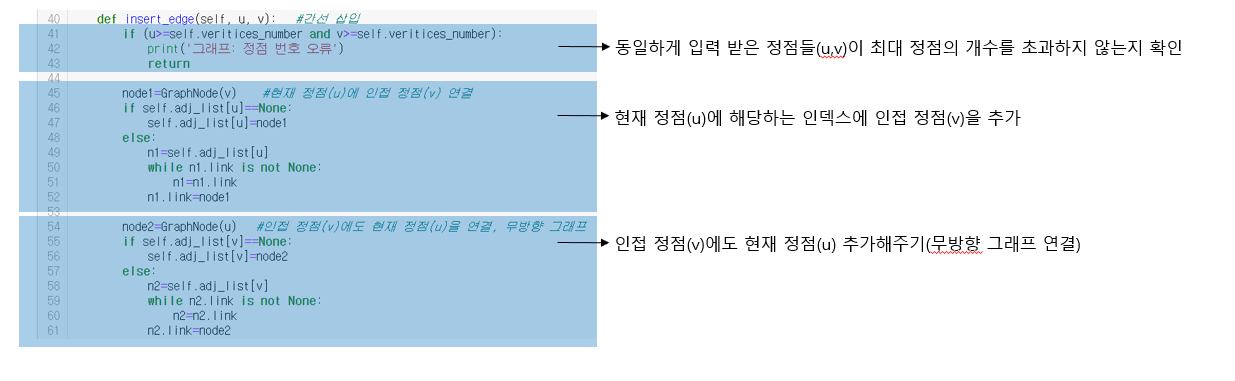
전체 코드로 보면 이런 구조다. 교재 코드는 이거 보다 간단한데 출력하면 너비 우선 탐색 같이 안 나와서 수정해버렸따!


인접 행렬 때와 동일하게 없는 정점들을 연결할 순 없기 때문에 if문을 통해 입력받은 정점이 현재 있는 정점의 번호를 초과하지 않는지 확인한다.

그리고 node1을 만들어준다. node1은 연결리스트로 인접 정점을 적는 vertex 필드와 다른 노드와 연결하기 위한 link필드가 있따. 현재 정점인 adj_list[u]는 현재 None이니까 바로 삽입해준다!

요기는 무방향 그래프를 표현하기 위해 인접 정점에도 현 정점의 노드를 만들어주는 과정이다. 인접 행렬에서도
adj_mat[start][end]
adj_mat[end][start]
요러케 둘에 True 값을 넣어주는 것이 무방향 그래프 만들기 위해서라고 설명햇엇쥬??
아무튼 요기도 adj_list[v]가 None이니까 바로 node2를 삽입해준다.
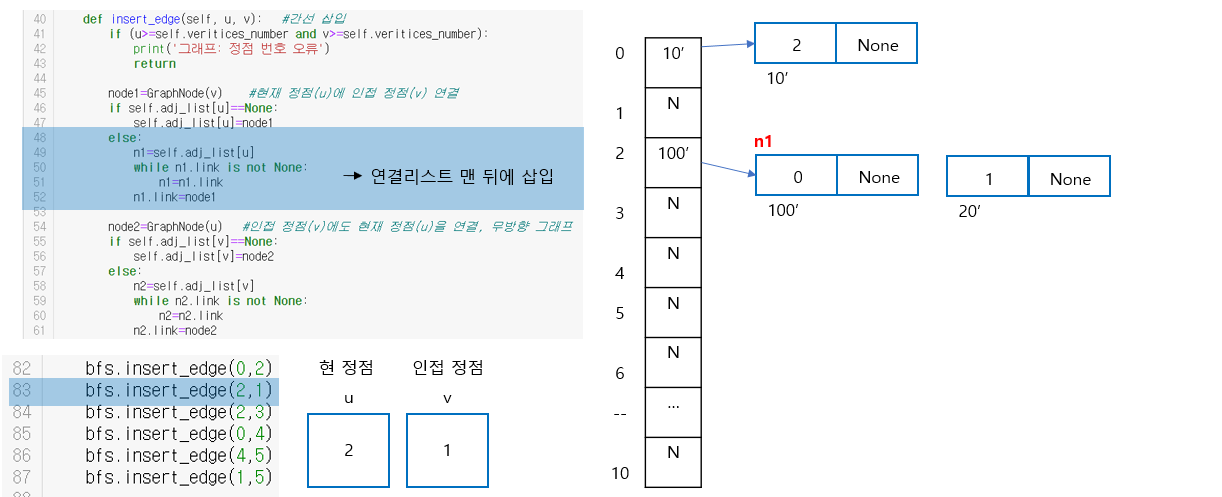
그 다음은 2,1은 받았는데, 현 정점인 2는 None이 아니므로 else문 실행! 연결리스트에서 노드 삽입할 때 연결리스트의 맨 뒤 노드에 삽입하는 코드이다. 아무튼 노드를 순회해서 맨 뒤 노드를 찾고 그 노드의 뒤에 새로운 노드를 붙여주면 끝이다!

요러케 다 연결하면 그림처럼 된다.. 노드 만들기 귀찮아서 수작업으로 만들었따.
<너비 우선 탐색>

너비 우선 탐색은 행렬 버전과 거~~의 유사하다.
1. 일단 현 정점을 vistied에 True표시하고 큐에 넣는다.
2. 큐가 비어있지 않으므로 while문을 실행할 수 잇다.
3. v에 큐에 있는 값을 dequeue하고
4. w에 현정점에 있는 연결리스트의 헤드 주소값을 넣는다
5. 순회하며 인접 정점들을 visited에 방문 표시 + 큐에 삽입
의 반복이다!!!
'python > 자료구조' 카테고리의 다른 글
| 문과생이 이해한 파이썬 Dijkstra의 최단 거리 알고리즘 (0) | 2021.09.15 |
|---|---|
| 문과생이 이해한 파이썬 Floyd의 최단 거리 알고리즘 (1) | 2021.08.31 |
| 문과생이 이해한 파이썬 BFS(너비 우선 탐색)- 인접 행렬 버전 (0) | 2021.08.17 |
| 문과생이 이해한 파이썬 연결리스트1-연습문제 (0) | 2021.07.29 |
| 문과생이 이해한 파이썬 연결리스트1(다항식 덧셈 프로그램) (1) | 2021.07.17 |



