[처음배우는딥러닝수학] 2장 01~04. 내가 수학을 논할 줄이야...

딥러닝 수업 듣는데 선형대수학이랑 최적화론, 자연어처리에서 배웠던 수학이 가물가물한 거 있죠. 수업 때 발표하는데 교수님 질문에 답변을 못하겠더라고요. 문제를 주면 풀 줄은 아는데 설명을 못 하는. 일명 메타인지가 덜 된 상태이죠.
항상 수학보다 지금 당장 하는게 더 급급하고 어느 정도 안다고 생각해서 안 했는데. 이번에 아슬아슬한 지식이란 걸 깨닫고 새로운 마음가짐으로 해봅니다.
교재는 <처음배우는딥러닝수학>입니다. 아쉽게도 확률과 통계가 없습니다. 그럼 시작해봅시다.
2장. 신경망을 위한 수학 기초
* 읽는 분이 딥러닝에 관한 지식이 있다고 가정합니다.
01. 신경망의 필수함수
1차/2차함수, 단위 계단/지수/시그모이드 함수, 정규 분포의 확률밀도함수
1. 1차 함수
신경망에서는 유닛이 받는 가중치를 1차 함수 관계로 표현한다.
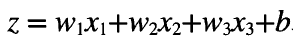
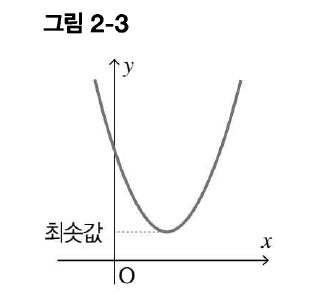
2. 2차 함수
실제 신경망에서는 변수가 더 많은 2차 함수를 다룬다고 한다. 2차 함수에서 알아둘 건, a가 양수일 때 아래로 볼록한 그래프이고 최솟값이 존재한다는 것이다. 이후 알아볼 최소제곱법의 기본이 된다.
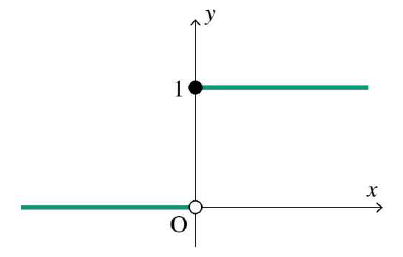
3. 단위 계단 함수
단위 계단 함수는 0 미만의 입력값은 모두 0으로 출력하고, 0 이상은 1로 출력한다.
- 원점에서 불연속-> 원점에서 미분 불가능함
- 원점에서 불연속/미분 불가능하다는 것은, 원점에서 값이 끊겨서 이어지지 않는다는 것을 의미한다. 그래프만 봐도 연속되지 않는다는 것을 알 수 있다.
- 이 미분 불가능하다는 특징 때문에 신경망의 활성화 함수로 자주 사용되지 않음
- 신경망은 경사하강법으로 모델을 학습하는데, 이 경사하강법은 미분을 사용한다. 어떤 지점에서 미분 불가능하면 이 경사하강법을 적용할 수 없기 때문에 신경망 활성화 함수로 사용되기에 적절하지 않다.
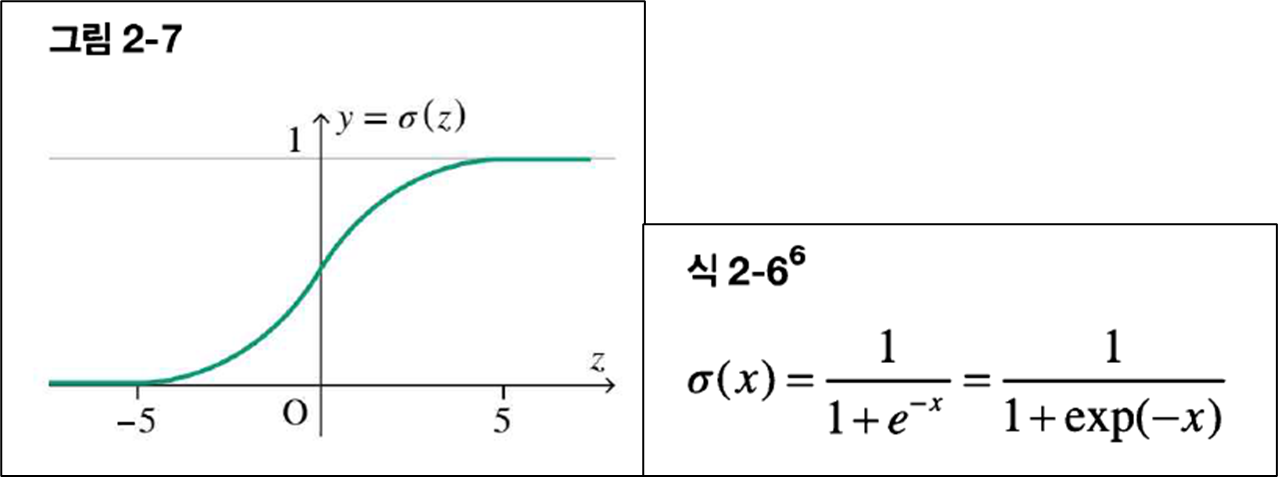
4. 지수 함수와 시그모이드 함수
지수 함수는 y=a^x 모양을 가진다.(a=밑) 밑의 값으로 특히 중요한 것은 자연 상수 e(약 2.7)이다.
이런 자연상수를 포함하는 지수함수를 분모로 갖는 함수가 바로 시그모이드 함수가 된다.
- 보다시피 어디서나 미분 가능한 함수임
- 함숫값은 0~1로, 확률을 계산할 수 있음
5. 정규분포의 확률밀도함수
신경망의 가중치 및 편향의 초깃값을 설정할 때 도움이 되는 것이 정규분포다. 이 분포를 따르는 정규분포 난수를 초깃값으로 사용하면 신경망 계산시 좋은 결과를 얻을 수 있다고 알려져 있다.
(정규 분포 수식 생략)
정규 분포 모양을 벨커브 모양(=종 모양)이라고 한다.
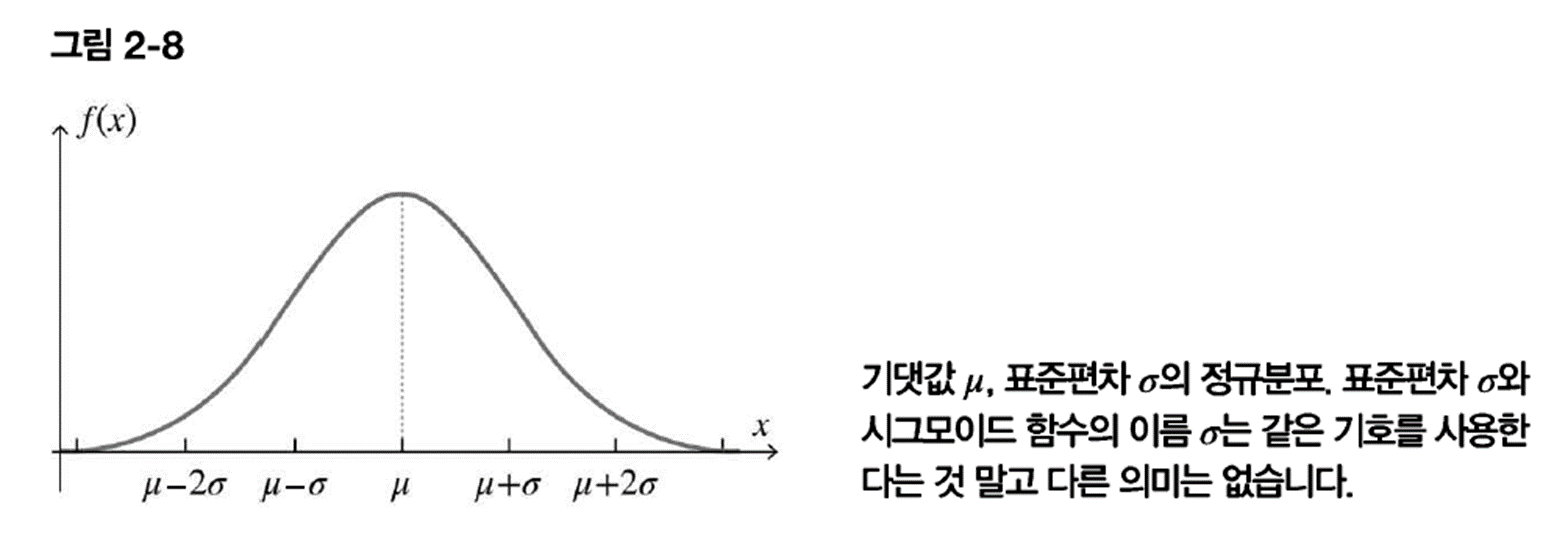
기댓값이 0이고, 표준편차가 1인 정규분포를 표준 정규분포라고 한다.
- 표준 정규 분포란 정규 분포를 규격화 시킨 것으로, 평균/표준편차 값에 따라 중심 위치 및 전체 모양(종 모양)이 달라져서 서로 비교하거나 확률 값 계산할 때 매우 불편해짐
- 그래서 모든 정규분포를 표준 정규분포로 변환하여 사용하는 것이 바람직하다고 함
- 어떻게 변환?
- 선형변환을 해줌. 선형변환은 데이터 그래프의 분포가 변하지 않는다는 특징이 있음
- z-score=x-기댓값 / 표준편차
- 선형변환?
- 동차성(Homogeneity, 同次性)- f(au) = af(u)
- 가산성(Additivity, 加算性)- f(u+v) = f(u) + f(v): 중첩(superposition) 가능하다고 함
- 한자는 정확한 건 아님. 말이 어려워서 찾아봄
Q. 가중치 초기화할 때 왜 정규 분포를 사용함?
- 일단 신경망의 파라미터가 모두 같으면, 학습을 하더라도 모두 같은 값으로 변함(여러 개의 노드를 구성한 의미가 없어짐)
- 따라서 무작위로 초기화를 해야 함
- 근데 진짜 단순하게 무작위 초기화를 할 경우 [-a, a] 사이의 난수를 뽑게 됨. 이 경우 일정 범위 내에서 난수를 선택하게 되므로 가중치들이 특정한 값에 몰리는 경향이 생김-> 이럴 경우 역전파 과정에서 기울기 폭발/소실 문제가 발생할 수 있음
- 정규 분포 난수를 사용할 경우, 초기 가중치들이 특정한 값에 몰리지 않고, 일정한 표준편차로 분포되어 있기 때문에, 학습이 안정적으로 이루어진다고 함
- 가중치 초기화에 사용되는 다양한 기법들은 아래 블로그를 참고하길 바람
https://yngie-c.github.io/deep%20learning/2020/03/17/parameter_init/
02. 신경망의 이해를 돕는 수열과 점화식
- 유한수열: 유한개 항 수를 갖는 수열-> 신경망에서 유닛의 가중 입력과 출력은 유한수열로 간주함
- 수열의 일반항: 주어진 수열의 n번째 수를 n을 이용한 식으로 나타낸 것
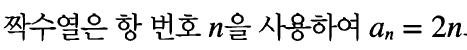
- 수열의 귀납적 정의: 이웃에 있는 항의 관계로 표현하는 방법-> 점화식이라고 함
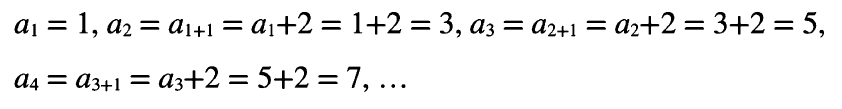
- 연립 점화식: 여러 수열이 몇 가지 관계식으로 연결된 것-> 신경망에서는 모든 유닛의 입력과 출력이 연립 점화식으로 연결되어있다고 생각함-> 이와 같은 점화식을 응용해서 오차역전파법을 수행함
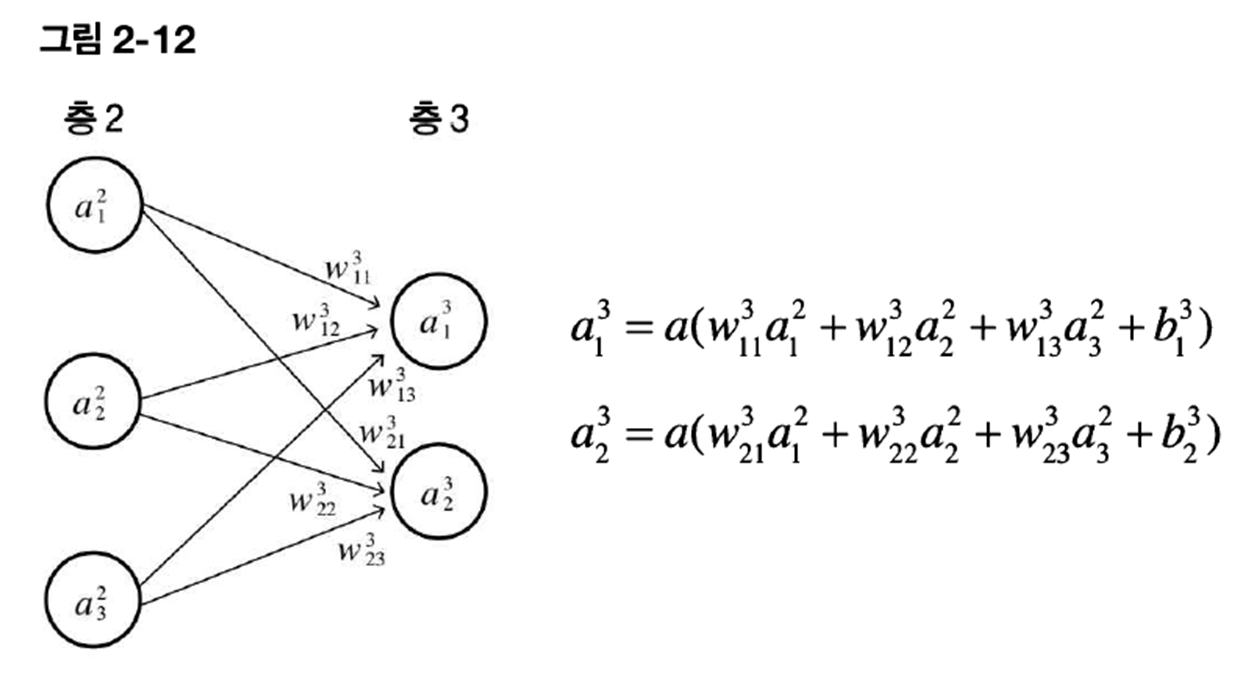
03. 신경망에서 많이 사용하는 시그마 기호
시그마( Σ )는 수열의 합 기호. 이는 선형성이라는 특징을 가짐. 위에서 말한 선형변환 특징과 같음.
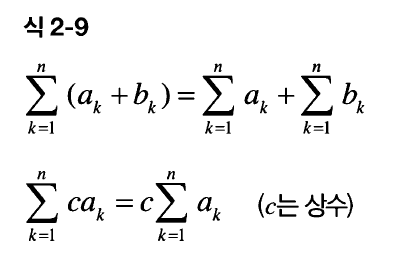
이게 왜 가능한지는 식을 풀어보면 알 수 있음.
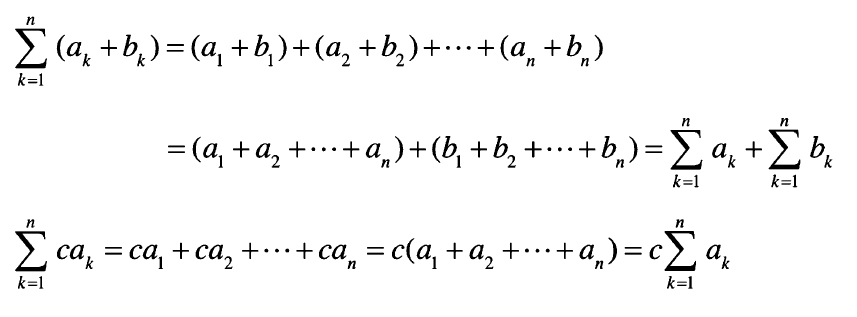
04. 신경망의 이해를 돕는 벡터
- 유향선분: 방향을 갖는 선분 A(시작점)B(종점).
- 유향선분은 점 A의 위치, B에 관한 방향, AB의 길이인 크기
- 벡터: 방향과 크기만을 추상화한 양
- 벡터의 성분 표시: 화살의 시작점을 원점에 놓고 종점의 좌표로 벡터를 나타내는 것
- 원점에 두는 건 점 A의 위치를 알 수 없기 때문이죠(당연한 소리)
- 뭔가 강아지 영역 표시 같고 좋네요...
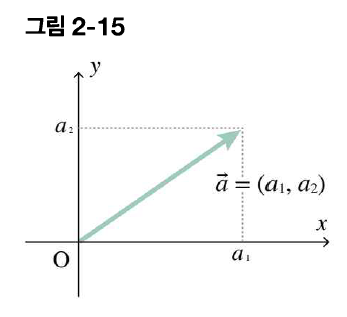
- 벡터의 크기: 화살표선의 길이, 스칼라 값을 가짐

- 벡터의 내적(Dot Product): 크기(스칼라)만 고려한 벡터의 곱셈-> 신경망의 입출력은 모두 벡터의 내적
- 두 벡터가 어느 정도로 같은 방향을 향하고 있는가?를 나타냄
- 벡터의 방향이 비슷하면 두 벡터의 내적은 커짐
- 코시-슈바르츠 부등식이 성립해야 함

| 0 | 30 | 45 | 60 | 90 | 120 | 180 | |
| COS | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -1 |
다음은 코시-슈바르츠 부등식이다.

2개의 벡터 크기를 일정하게 하면 관계는 아래 3가지가 된다.

- 내적의 성분 표시

- 벡터의 일반화: 벡터의 편리한 점은 평면과 입체 공간의 특징을 임의의 차원에 그대로 확장할 수 있다는 것
기본적인 수학이라 어렵진 않았고, 애매했던 개념이 잡힌 것 같네요. 사실 진도 나가는 건 괜찮은데 옮겨적는 게 헬이에요. 빨리빨리 진도 나가고 싶은데, 맘처럼 쉽지 않군요. 아무튼 감사합니다.
끗!